Эксперт

Сергей

Задать вопрос

Мы готовы помочь Вам.

Задача 1. Определить натуральную величину расстояния от точки S до плоскости Г(АВС) способом прямоугольного треуголь-ника.
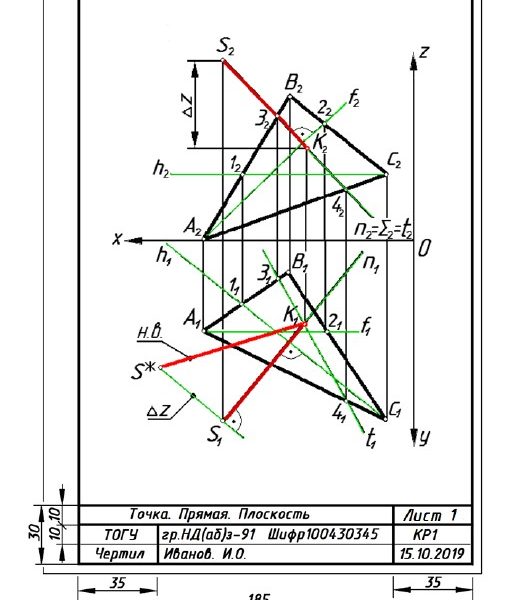
Индивидуальные варианты к задаче 1 приведены в табл. 3. По-следовательность решения задачи 1 поэтапно показана на рис. 2. Пример оформления листа 1 представлен на рис. 3.

Указания к решению задачи 1
Из табл. 2 согласно варианту выбрать координаты точек S, А, В, С и построить их проекции на двухкартинном комплекс-ном чертеже. Проекции точек А, В и С последовательно соединить отрезками прямых, чтобы получились проекции плоскости Г, заданной треугольником АВС.
Расстояние от точки до плоскости есть длина перпендикуляра, построенного от точки к плоскости.
Прямая перпендикулярна плоскости, если она перпендику-лярна двум пересекающимся прямым этой плоскости. В качестве этих прямых должны быть взяты линии уровня, так как согласно теореме о проецировании прямого угла прямой угол проециру-ется без искажения на плоскость проекций, если одна из его сто-рон параллельна этой плоскости, другая не перпендикулярна ей. Проведённые в плоскости линии уровня будут играть роль сто-рон, параллельных заданной плоскости, и прямой угол можно строить на чертеже в натуральную величину.
План решения задачи 1
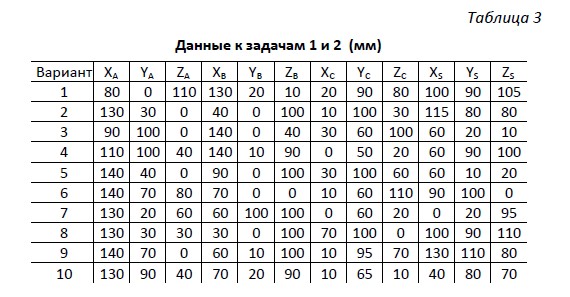
1. В плоскости Г(АВС) проводим фронтальную прямую уровня f(f1,f2) и горизонтальную прямую уровня h(h1,h2) (рис. 2, ①).
2. Из точки S(S1, S2) проводим проекции перпендикуляра к плос-кости Г(АВС): на П1 n1  h1, на П2 n2  f2 (рис. 2, ②).
3. Определяем точку К(К1, К2) пересечения перпендикуляра n(n1, n2) с плоскостью Г(АВС) (рис. 2, ③).
3.1. Заключаем прямую n во фронтально-проецирующую
плоскость Σ(Σ2):
n2 = Σ2 = t2.
3.2. Проводим линию t пересечения плоскостей Σ и Г: t(t1, t2).
3.3. Находим проекции точки К(К1, К2) пересечения прямой n
с плоскостью Г(АВС):
t1 n1= К1; К2 n2.
4. Определяем натуральную величину расстояния от точки S до
плоскости Г(АВС) способом прямоугольного треугольника (рис. 2, ④) :
н.в.SK = S*K.

Задача 2. Определить угол наклона плоскости Г к горизонталь-ной плоскости проекций способом прямоугольного треугольника
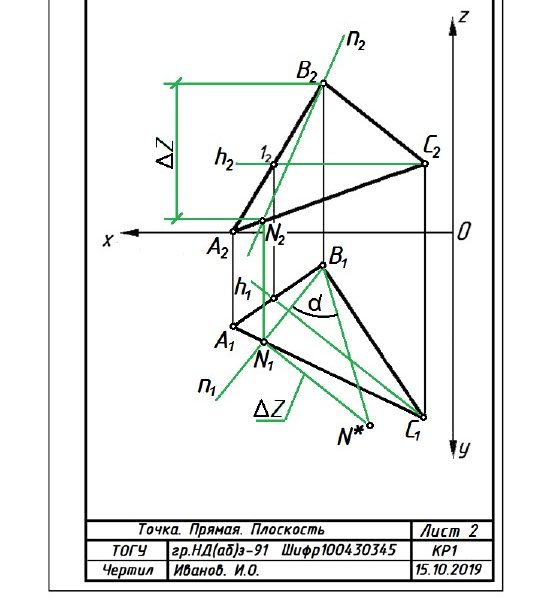
Индивидуальные варианты к задача 2 приведены в табл. 3. Пример оформления листа 2 представлен на рис. 4.
Угол наклона плоскости к какой-либо плоскости проекций можно определить при помощи линии наибольшего уклона.
Линией наибольшего уклона плоскости называются прямая, лежащая в ней и перпендикулярная линиям уровня плоскости.
Линия наибольшего уклона к горизонтальной плоскости про-екций называется линией ската – это прямая n, принадлежащая какой-либо плоскости (Г) и перпендикулярная ее горизонтали h. Угол α наклона линии наибольшего ската к плоскости П1 опреде-ляет наклон плоскости Г к плоскости П1.
План решения задачи 2
1. Построить горизонталь в плоскости треугольника АВС.
В плоскости Г(АВС) проводим горизонталь h(h1,h2) (рис. 4).
h2(С212)  Г2(А2В2С2), h1(С111), h(h1,h2)  Г(АВС).
2. Построить проекции линии ската в плоскости АВС.
В плоскости Г(АВС), например через точку В(В1), строим проекцию линии ската n(n1). Горизонтальная проекция линии ската n1 перпендикулярна горизонтальной проекции h1 плос-кости. Обозначаем вторую точку N1 и строим фронтальную проекцию линии ската: n1  h1, n2(В2N2)  Г2(А2В2С2).
3. Определить угол наклона линии ската n к плоскости проекций П1.
Возьмем любой отрезок (ВN) на линии ската и способом прямоугольного треугольника определим его натуральную величину. Угол между гипотенузой B1N* и проекцией отрезка B1N1 является углом наклона линии ската BN к плоскости про-екций П1. Тогда углом наклона α плоскости Г(АВС) к горизон-тальной плоскости проекций является угол N1B1N* – между натуральной величиной линии ската и ее горизонтальной про-екцией: N1B1N* = α = Г(АВС) ˄

Задача 3. Через заданную точку N, принадлежащую поверх-ности конуса, провести проецирующую плоскость Σ, пересекаю-щую конус по указанной в варианте линии и построить линию пересечения конуса с плоскостью.
Индивидуальные варианты к задачам 3, 4 приведены на рис. 5. Пример оформления представлен на рис. 6.

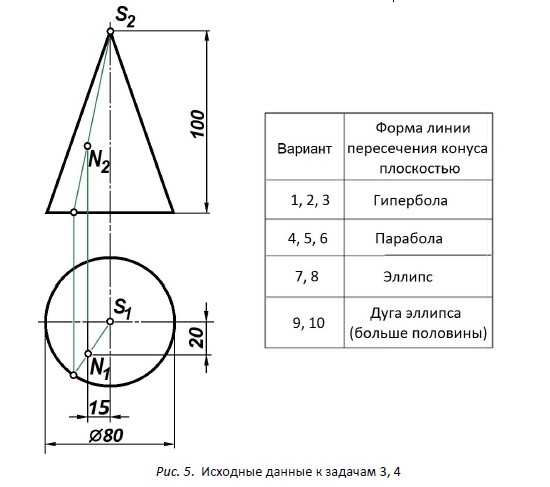
Рис. 5. Исходные данные к задачам 3, 4
Рассмотрим для примера вариант решения задачи, в которой требуется получить в сечении конуса дугу эллипса.
16
План решения задачи 3
1. Построение проекций конуса и секущей плоскости Σ в си-стеме плоскостей проекций П1/П2.
2. Построение проекций линии пересечения конуса задан-ной плоскостью на основных плоскостях проекций.
3. Определение видимости линии пересечения.
РЕШЕНИЕ:
1. Намечаются оси координат и согласно варианту на П1 строится окружность основания конуса диаметром 80 мм (рис. 6) и горизонтальная проекция точки N(N1). На П2 строится основание конуса, вершина конуса на вертикальной оси Z на высоте h=100 мм от плоскости основания, фронтальный очерк конуса и фрон-тальную проекцию точки N(N2).
В задаче требуется провести через точку N проецирующую плоскость таким образом, чтобы в сечении получилась дуга эл-липса. Эллипс получается в сечении, если плоскость пересекает все образующие конуса и не перпендикулярна к его оси. Дуга эл-липса получится, если секущая плоскость будет так же пересекать образующие конуса и его основание. Через точку N(N2) проводим фронтально-проецирующую плоскость Σ(Σ2) так, чтобы она пересекла основание.
2. Полученная секущая плоскость Σ(Σ2) перпендикулярна фронтальной плоскости проекций и её след обладает собира-тельным свойством. Линия пересечения в таком случае на фрон-тальной плоскости проекций совпадает со следом секущей плос-кости, имеет вид отрезка, ограниченного точкой 1(12), находя-щейся на очерковой образующей, и точками 2(22) и 3(32), находя-щимися в основании конуса. Горизонтальные проекции 11, 21 и 31 построены при помощи линий связи. Точка 1 является наивыс-шей, а точки 2 и 3 – низшими характерными (опорными) точками линии сечения, лежащими в плоскости основания Ф(Ф2).
Для построения линии пересечения отмечены промежуточ-ные точки на фронтальной проекции линии пересечения: N2 ≡ 42, 52 ≡ 62, 72 ≡ 82 и 92 ≡ 102. Для их определения вводятся вспомога-тельные горизонтальные плоскости уровня Т(Т2), Г(Г2), Δ(Δ2),
17
Рис. 6. Пример оформления задач 3, 4
18
которые пересекают конус по окружностям, а секущую плоскость – по прямым. Пересечения полученных окружностей с соответ-ствующими прямыми дают горизонтальные проекции этих точек: 41, 51, 61, 71, 81, 91 и 101.
3. Полученные точки соединяются плавной линией. Вся линия пересечения (31 – N1 – 51 – 71 – 91 – 11 – 101 – 81 – 61 – 41 – 21) на горизон-тальной плоскости проекций является видимой, т.к. находится на видимой боковой поверхности конуса.
Относительно фронтальной плоскости проекций видима пе-редняя часть поверхности конуса, находящаяся ближе верти-кальной плоскости симметрии Ѱ (Ѱ1) предмета, и линия на ней – видима, но линия пересечения тоже симметрична, значит, фрон-тальные проекции видимой и невидимой части линии пересече-ния на П2 совпадают.
Задача 4. Определить натуральную величину сечения конуса плоскостью Σ способом замены плоскостей проекций
План решения задачи 4
1. Преобразование комплексного чертежа.
2. Построение проекции сечения конуса секущей плоскостью в новой системе плоскостей проекций П2/П5.
РЕШЕНИЕ:
1. Чтобы построить проекцию действительной величины сече-ния конуса секущей плоскостью, следует преобразовать ком-плексный чертёж так, чтобы секущая плоскость Σ(Σ2) в новой си-стеме плоскостей проекций заняла положение плоскости уровня. В этом случае линия пересечения будет проецироваться в нату-ральную величину. Для этого удобно применить способ замены плоскостей проекций: П1/П2 → П2/П5. Новая ось Х2,5 проводится па-раллельно проекции плоскости Σ2: Х2,5 II Σ2.
Теперь в системе плоскостей проекций П2/П5 плоскость Σ за-нимает положение плоскости уровня по отношению к плоскости проекций П5.
19
С целью облегчения построений «старую» ось Х между П1 и П2 рационально провести через центр основания конуса: Х1,2, т. к. линия сечения на П1 симметрична относительно этой оси.
2. Для построения линии пересечения найдена точка середи-ны отрезка 12 – 1ʹ2 , являющегося большей осью эллипса, здесь будут находиться опорные точки ближайшая и наиболее удалён-ная от наблюдателя (52 ≡ 62). От фронтальных проекций каждой точки линии пересечения: 12, 22 ≡ 32, N2 ≡ 42, 52 ≡ 62, 72 ≡ 82 и 92 ≡ 102 проводятся новые линии связи перпендикулярно оси Х2,5 для новой системы плоскостей проекций П2/П5.
В новой плоскости П5 строится проекция сечения конуса плос-костью Σ с сохранением соответствующих глубин каждой точки, полученных на П1, которые измеряются от оси Х1,2 и откладыва-ются от оси Х2,5 по новым линиям связи. Линия сечения обводится плавно по точкам 35 – N5- 55 – 75 – 95 – 15 – 105 – 85 – 65 – 45 – 25 – это и есть натуральная величина сечения.
Лист 4. «Проекции с числовыми отметками»
Задача 5. Построить линии пересечения откосов выемок и насыпей земляного сооружения (площадки) между собой и с то-пографической поверхностью, приняв уклон откосов выемок 1:1, уклон откосов насыпей 1:1,5.
Форму земляного сооружения и угол наклона оси сооружения определяют по номеру варианта из табл. 4.
Пример оформления представлен на рис. 7.
Таблица 4
Для выполнения графической работы необходимо начертить на листе формата А4 в масштабе 1:200 план земельного участка,

Рис. 7. Пример оформления задачи 5
рельеф которого задан горизонта-лями (рис. 8) и нанести на него в том же масштабе план земляного сооружения так, чтобы центр со-оружения О совпал с центром участка О, и ось сооружения была наклонена к меридиану под за-данным углом. Планы земляных сооружений изображены на рис. 9.
Рис. 8. Рельеф земельного участка
Рис. 9. Планы земляных сооружений
Указания к оформлению работы
Графическую работу выполняют на чертежной бумаге формата А4 карандашом. Горизонтали топографической поверхности об-водят тонкими линиями толщиной 0,1 – 0,2 мм. Контуры земля-
ного сооружения и линии пересечения откосов с топографиче-ской поверхностью и между собой обводят карандашом линиями толщиной 0,4 – 0,6 мм. Бергштрихи откосов выемок и насыпей выполняют линиями толщиной 0,1 – 0,2 мм их проводят перпен-дикулярно проектным горизонталям при расстоянии между штрихами 1,5 – 2,5 мм. Линии построения (в том числе проектные горизонтали) должны иметь толщину 0,1 – 0,2 мм.
При решении задачи 5 следует исходить из основных положе-ний темы «Проекции с числовыми отметками».
Построение линии пересечения плоскости и поверхности или двух поверхностей выполняется по точкам пересечения одно-значных горизонталей обеих поверхностей (или плоскости и по-верхности). На рис. 10 показано пересечение плоскости и по-верхности. Поверхность задана горизонталями, плоскость – мас-штабом уклона Pi.
Рис. 10. Построение линии пересечения плоскости и поверхности, заданной горизонталями
Решение основных позиционных задач в проекциях с числовыми отметками
Для выполнения задания необходимо твердо знать графиче-ские способы решения ряда задач, приведенных в настоящем разделе.

Задача. Определить границы насыпи и выемки при проекти-
ровании горизонтальной строительной площадки (рис. 11).
Рис. 11. Строительная площадка
Решение:
1. Сравним отметку площадки с отметками горизонталей то-
пографической поверхности.
2. Установим, что левая часть площадки будет находиться в
выемке, а правая – на насыпи.
3. Горизонталь поверхности земли, имеющая одинаковую с
площадкой отметку +22,000 м и расположенная с ней на одном
уровне, называется линией нулевых работ.
4. Точки А и В, в которых линия нулевых работ пересекается с
бровками площадки, называются точками нулевых работ и яв-
ляются точками раздела насыпи и выемки.
Задача. Построить линию пересечения смежных откосов
насыпи строительной площадки с отметкой +22,000 м. Уклон
плоскости откоса насыпи
iн = 1:1,5; масштаб чертежа 1:200 (рис. 12).
Решение:

На рис. 12 фрагмент горизонтальной строительной площадки ограничен бровкой – линией земляного сооружения, от которой начинается боковой откос насыпи. Бровки площадки являются горизонталями с отметкой +22,000 м.
Рис. 12. Строительная площадка
1. Заключаем бровки площадки в плоскость общего положе-ния, которая задается масштабом уклона плоскости.
2. Масштабы уклонов и проводим перпендикулярно бровкам площадки.
3. Определяем величину интервалов горизонталей масшта-бов уклонов и с учетом масштаба чертежа 1:200:
В масштабе 1:200 = 0, 75 см.
4. Градуируем масштабы уклонов и через интервал горизон-талей плоскостей = 0, 75 см. По насыпи отметки горизонталей бу-дут понижаться. Через полученные отметки проводим горизон-тали плоскостей 21, 20, 19, 18 и т. д.
5. Искомые линии пересечения плоскостей откосов между со-бой строительной площадки строятся по точкам пересечения од-ноименных горизонталей. Для построения прямой достаточно определить две точки. Для плоских откосов с одинаковыми

уклонами насыпи, это будут прямые линии – биссектрисы углов, образованных горизонталями плоскости откоса.
Задача. Построить линию пересечения откоса полукруглого выступа площадки с плоскостью откоса насыпи.
Уклон откосов = 1:1,5; масштаб чертежа 1:200; (рис. 13).
Рис. 13. Линия пересечения откоса Рис. 14. Линия касания откоса
полукруглого выступа площадки полукруглого выступа площадки
с плоскостью откоса насыпи с плоскостью откоса насыпи
Решение:
1. Откос полукруглого выступа имеет форму конической поверхности. Через точку S – вершину конуса, проведем градуи-рованную образующую – т. е. проекцию линии наибольшего уклона поверхности Pi.
2. Проведем масштаб уклона Σi плоскости откоса насыпи.
3. Проградуируем масштабы уклонов Pi и Σi с интервалом lH = 1,5 м; в масштабе 1:200 lH = 0, 75 см.
4. Через полученные отметки Pi и Σi проведем горизонтали. Горизонталями конической поверхности являются концентриче-ские окружности с центрами, совпадающими с вершиной S.
5. Находим точки пересечения одноименных горизонталей и соединяем их плавной кривой, которая является искомой линией пересечения (рис. 13).

В случае одинакового уклона плоскости откоса и образующих конуса искомая линия – парабола (рис. 14).
В другом случае, если бровка плоского откоса площадки касается бровки поверхности конуса строительной площадки,
имеющие одинаковые уклоны насыпи, то и одноимённые гори-зонтали масштабов уклонов Pi и Σi будут касаться друг друга. По-этому линия М22К22 – образующая конуса, является линией каса-ния, которая не проводится на чертеже (рис. 14).
Задача. Построить линию пересечения откосов насыпи строи-тельной площадки с отметкой +22,000 м с топографической по-верхностью.
Уклон i Н = 1:1,5; масштаб чертежа 1:200; (рис. 15).
Рис. 15. Линия пересечения смежных откосов, если поверхность релье-фа пересекается двумя плоскостями, имеющими общее ребро
Решение:
1. Проводим масштабы уклонов Pi и Σi перпендикулярно бровкам площадки.

2. Определяем величину интервалов горизонталей масштабов уклонов с учетом масштаба чертежа lH = 0,75 см.
3. Градуируем масштабы уклонов через lH = 0,75 см и прово-дим горизонтали. В насыпи отметки горизонталей плоскостей понижаются. Таким образом, плоскость каждого откоса опреде-лена.
4. Искомые линии пересечения плоскости каждого откоса с топографической поверхностью находим по точкам пересечения одноименных горизонталей плоскости и топографической по-верхности. Эти линии определяют границу земляных работ.
Следует отметить, если поверхность рельефа пересекается двумя плоскостями, имеющими общее ребро, то линии пересе-чения смежных откосов с рельефом местности должны пересе-каться между собой обязательно на этом ребре в точке М (рис. 15).
Для уточнения расположения точки М на ребре необходимо найти вспомогательные точки «а» и «б» на дополнительных го-ризонталях при их продолжении за ребро.
5. Для наглядности изображения границ земляных работ ли-нии бровки площадки выделяются бергштрихами, которые пока-зывают направление ската воды. Они выполняются чередующи-мися штрихами разной величины тонкими сплошными линиями.
Построение границ земляных работ в выемке аналогично по-строению земляных работ в насыпи. Необходимо обратить вни-мание на то, что строительная площадка имеет уклон iВ = 1:1 , масштаб чертежа 1:200. Для решения тех же задач в выемке необ-ходимо рассчитать интервал горизонталей плоскостей откосов,
в масштабе чертежа lв = 0,5 см.
Используя этот интервал, студенты самосто