Задание 1.1

Решить задачу, условие которой приводится далее. Значения постоянных величин для решения по вариантам сведены в таблицы 1 и 2.

Рекомендации по выполнению задания приведены в разделе «Краткие теоретические сведения».

Методом наименьших квадратов для данных, представленных в таблицах 1 и 2, найти линейную зависимость y = ax + b.

 

 

Таблица 1

Вариант	y1	y2	y3	y4	y5	y6	y7	y8
1	15,23	10,42	7,12	3,10	−0,39	−4,19	−7,37	−11,14
2	13,72	9,39	6,41	2,79	−0,43	−4,65	−8,18	−12,37
3	12,59	8,61	5,88	2,56	−0,47	−5,07	−8,92	−13,48
4	9,66	4,85	1,55	−2,47	−5,96	−9,76	−12,94	−16,71

Таблица 2

i	1	2	3	4	5	6	7	8
xi	5	4	3	2	1	0	−1	−2

Образец выполнения задания 1.1

Методом наименьших квадратов для данных, представленных в таблице 3, найти линейную зависимость y = ax + b.

Таблица 3

i	1	2	3	4	5	6	7	8
xi	5	4	3	2	1	0	−1	−2
yi	14,08	10,12	6,91	3,01	−0,41	−4,32	−7,59	−11,47

Параметры a и b можно найти методом наименьших квадратов, решив следующую систему уравнений:

,                                                                (1)

где суммирование ведется по i от 1 до n, n = 8. Составим расчетную таблицу 4.

Таблица 4

i	1	2	3	4	5	6	7	8	Сумма
xi	5	4	3	2	1	0	−1	−2	12
yi	14,08	10,12	6,91	3,01	−0,41	−4,32	−7,59	−11,47	10,33
	25	16	9	4	1	0	1	4	60
xiyi	70,4	40,48	20,73	6,02	−0,41	0	7,59	22,94	167,75

Получаем следующую систему:

,                                                                     (2)

откуда находим a = 625,3 , b=146,4, то есть получаем функцию

y = 3,625x − 4,146.

Задание 1.2

Решить задачу, условие которой приводится далее. Значения постоянных величин для решения по вариантам сведены в таблице 5.

Рекомендации по выполнению задания приведены в разделе «Краткие теоретические сведения».

Прибыль фирмы за некоторый период деятельности по годам приведена в таблице 5.

Таблица 5

Вариант № 1	Год	1	2	3	4	5
	Прибыль	3,5	4,5	3,0	1,0	1,5
Вариант № 2	Год	1	2	3	4	5
	Прибыль	2,9	3,9	2,4	0,4	0,9
Вариант № 3	Год	1	2	3	4	5
	Прибыль	2,5	3,4	2,2	1,5	0,7
Вариант № 4	Год	1	2	3	4	5
	Прибыль	4,0	5,0	3,5	1,5	2,0

1. Составьте линейную зависимость прибыли по годам деятельности фирмы.
2. Определите ожидаемую прибыль для 6-го года деятельности. Сделайте график полученной функции и нанесите точки, обозначенные в исходных данных.

Образец выполнения задания 1.2

Прибыль фирмы за некоторый период деятельности по годам приведена в таблице 6.

Таблица 6

Год	1	2	3	4	5
Прибыль	3,9	4,9	3,4	1,4	1,9

Обозначим прибыль как y, а год как x. Параметры a и b линейной зависимости y = at + b можно найти методом наименьших квадратов из следующей системы уравнений:

,                                                                 (3)

где суммирование ведется по i от 1 до 5. Составим расчетную таблицу 7.

Таблица 7

						Сумма
ti	1	2	3	4	5	15
yi	3,9	4,9	3,4	1,4	1,9	15,5
	1	4	9	16	25	55
tiyi	3,9	9,8	10,2	5,6	9,5	39

Получаем следующую систему:

(4)

Отсюда находим, что a = −0,75, b = 5,35, то есть получаем функцию

y = −0,75t + 5,35.

Определим ожидаемую прибыль от 6-го года деятельности:

y₆ = −0,75 • 6 + 5,35 = 0,85.

Построим точки и линию y = −0,75t + 5,35 на одном графике (рис. 1).

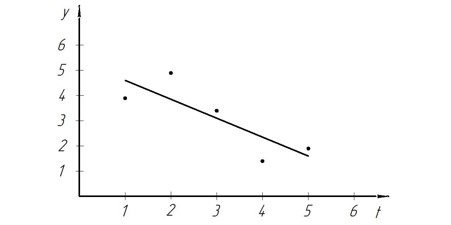
Рис. 1. График функции y(t)