Пример выполнения задания.

Дана матрица смежности взвешенного орграфа.

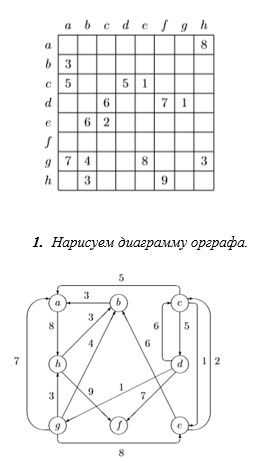
2 Найдем кратчайшие пути между всеми парами вершин, используя волновой алгоритм. Выберем все поочередно узлы в качестве стартовых. Ход решения изобразим в виде дерева, в котором узлы с одним номером волны поместим одну под другой, а узлы с большим номером волны – правее, чем вершины с меньшим номером.

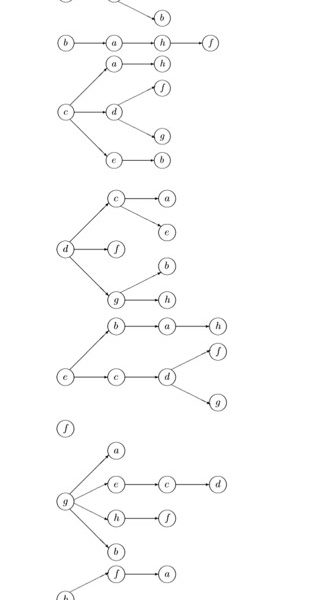
Построим матрицу кратчайших путей. Элемент матрицы (u, v) представляет собой кратчайший путь < u, v >, если пути не существует, в соответствующей клетке ставится прочерк. В последнем столбце выпишем максимальные уклонения от узлов.

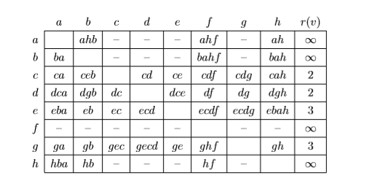
3 Определим тип связности орграфа. Из матрицы кратчайших путей видно, что для любых узлов u, v существует либо путь < u, v >, либо путь < v, u >, т. е. орграф является односторонне связным.

 

Построим фактор-граф орграфа. Выделим компоненты сильной связности, объединив в каждой компоненте все сильно связные между собой узлы.

A = {a,b,h};

C = {c,d,e,g};

F = {f}.

Стянув каждую компоненту в узел, получаем фактор-граф.

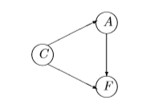
4 Определим диаметр, радиус и центр орграфа. Диаметр равен наибольшему из максимальных удалений, т.е. D = ∞. Радиус равен наименьшему из максимальных удалений, т. е. r = 2. Центрами являются узлы, максимальное удаление от которых равно радиусу, т. е. c и d.

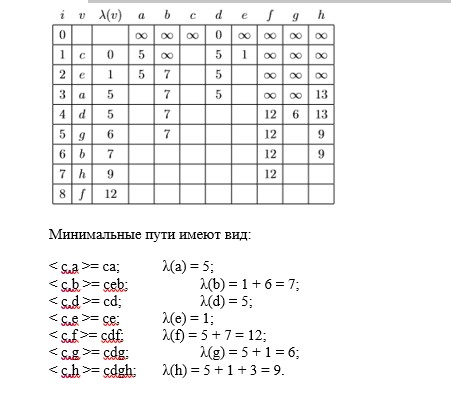
5 Найдем минимальные пути от центра c до остальных узлов алгоритмом Дейкстра. Решение оформим в виде таблицы. Здесь столбец i содержит номер итерации, столбец v –текущий узел, столбец λ(v) –вес минимального пути от стартового узла до текущего. В столбцах a–h содержатся метки неокрашенных узлов – наименьшие веса путей, найденные на текущей итерации. Узел с минимальной пометкой назначается текущим на следующей итерации.

1. Найдем кратчайшее остовное дерево графа алгоритмом Краскала. На рисунке изображен кратчайший остов, справа выписан порядок его построения.
2. Определим, является ли соответствующий неориентированный граф эйлеровым (полуэйлеровым). Если отменить ориентацию ребер, две вершины– c и g –имеют нечетную степень. Построим эйлерову цепь алгоритмом Флери, начиная с вершины c. На рисунке ребра отмечены в порядке прохождения.

​Эйлерова цепь имеет вид cecdcagebahfdgbhg.

3. Определим, является ли соответствующий неориентированный граф гамильтоновым (полугамильтоновым). Гамильтонов цикл имеет вид agecdfhba. Значит, граф гамильтонов.
4. Уложим неориентированный граф без кратных ребер на плоскости. Рассмотрим диаграмму графа.

Выделим цикл bgdfhb и уложим его на плоскости без пересечений. Получили укладку с двумя гранями. Имеются два сегмента, каждый из которых может быть уложен в любую грань. Контактные вершины сегментов обведены двойной линией

​

Укладываем сегмент gh в Γ₁. Получили укладку с тремя гранями и один сегмент, все контактные вершины которого h, b, g, d принадлежат одновременно лишь границе Γ₂.

 

​

Выбираем α-цепь bacd и укладываем ее в грань Γ₂.

Получили укладку с четырьмя гранями и три сегмента, допустимые грани для них указаны в скобках. Укладываем сегмент ag в Γ₄.

Получили укладку с пятью гранями и два сегмента, для одного из которых нет ни одной допустимой грани (все его контактные вершины b, c, g не принадлежат одновременно ни одной из границ граней). Плоская укладка невозможна, граф не является планарным.

Этот результат можно получить иначе, построив подграф исходного графа, гомеоморфный K3,3. Здесь {a, e, d} – первая доля, {b, c, g} – вторая доля, K3,3 получается удалением вершин f и h степени 2.

5. Найдем минимальную раскраску неориентированного графа. Рассмотрим диаграмму графа (без кратных ребер). Для раскраски используем идею алгоритма «по цветам». Выделим произвольное максимальное независимое множество вершин {a, d, e} и раскрасим в первый цвет (обведены двойной линией). Затем выделим произвольное максимальное независимое множество неокрашенных вершин {b, c, f} и раскрасим во второй цвет (обведены квадратом). Снова выделим произвольное максимальное независимое множество неокрашенных вершин {h} и раскрасим в третий цвет (обведена ромбом). Оставшуюся вершину g красим в четвертый цвет.

​

Раскраска в 4 цвета является минимальной, так как граф содержит K4, построенный на вершинах {a, b, g, h}, в качестве подграфа.