Цель     работы:  ознакомиться с классификацией кинематических пар и механизмов, выполнить структурный анализ.

 

СОДЕРЖАНИЕ И ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ

 

1. Выполнить эскиз кинематической пары.
2. Определить класс кинематической пары и название по типу ка-

 

сания звеньев и соединения их в пару.

3. Определить степень подвижности механизма.
4. Определить класс и порядок механизма.

 

 

КИНЕМАТИЧЕСКАЯ  ПАРА

Соединение двух соприкасающихся звеньев, допускающее их  от- носительное движение, называется кинематической парой.

Для кинематических пар характерны следующие признаки: классы, элементы касания звеньев, типы соединения звеньев в  пару.

 

 

1. Классы

Класс кинематической пары определяется числом ограниченных степеней свободы (S). Таким образом, у пар 1-го класса ограничена одна степень свободы, у пар 2-го класса – две степени свободы и т.д.

S = 6 – H,

где Н – число движений звеньев, входящих в пару.

 

 

2. Элементы касания звеньев

Если элементом касания звеньев является точка или линия, то па- ра называется высшей.

Если элементом касания является плоскость или поверхность, то пара называется низшей.

 

3. Тип соединения звеньев в пару

Пара называется геометрически замкнутой, если соединение звеньев обеспечивается их конструкцией.

Пара будет иметь силовое соединение, если контакт    элементов обеспечивается под действием силы.

 

Звенья в механизме соединяются между собой кинематическими парами. Если соединяются два звена, то будет одна кинематическая пара. Если соединяются три звена, то будет две кинематических пары. Если соединяются n звеньев, то будет n–1 кинематических пар (слож- ный шарнир).

В табл. 1 приведены схемы и  условные обозначения наиболее ча- сто встречающихся видов кинематических пар.

 

Таблица 1

Пространственная схема (пример)	Условное обозначение	Кинематическая пара
Шар на плоскости		Точечная кинематическая пара 1-го класса с силовым замыканием, высшая
Цилиндр на плоскости		Кинематическая пара 2-го класса с силовым замыканием, высшая
Призма на плоскости		Кинематическая пара 3-го класса с силовым замыканием, низшая
Сферическая		Сферическая кинематическая пара 3-го класса с геометрическим замыканием, низшая
Сферическая с пальцем		Кинематическая пара 4-го класса с геометрическим замыканием, низшая
Цилиндрическая		Цилиндрическая кинематическая пара 4-го класса с геометрическим замыканием, низшая

 

Продолжение табл. 1

Пространственная схема (пример)	Условное обозначение	Кинематическая пара
Вращательная		Вращательная кинематическая пара 5-го класса  с геомет- рическим      замыкани- ем, низшая
Поступательная		Поступательная кинематическая пара 5-го класса с геометрическим         за- мыканием, низшая
Винтовая		Винтовая кинемати- ческая пара 5-го класса с геометриче- ским замыканием, низшая

 

МЕХАНИЗМ

Принцип образования механизмов был впервые сформулирован выдающимся русским ученым профессором Л. В. Ассуром в 1914 г.

Он состоит в следующем:

любой механизм может быть образован путем последовательного присоединения к входному звену и стойке кинематических цепей с ну- левой степенью подвижности (группы Ассура).

Известно, что в состав каждого механизма входят: неподвижное звено (стойка), входные звенья, законы движения которых заданы, вы- ходные звенья, законы движения которых зависят от законов движения входных звеньев, а также могут входить промежуточные звенья.

Рычажный механизм состоит из звеньев:

 

Звенья рычажного механизма:

• ползун – совершает возвратно-поступательное движение;
• кривошип – совершает вращательное движение (полный оборот вокруг неподвижной оси);
• шатун – совершает сложное плоскопараллельное движение (зве- но, образующее кинематические пары только с подвижными звеньями);
• коромысло (качающееся звено) – совершает неполный оборот вокруг оси;
• кулиса – звено совершающее поступательное, вращательное или качательное движение, по которому перемещается кулисный ка-

 

мень;

• камень –  звено  кулисного  механизма,  совершающее поступа-

 

тельное движение относительно кулисы (в случае качающегося камня кулиса движется поступательно относительно камня);

– стойка – неподвижное звено любого механизма.

 

 

Если входное звено не задано, то его можно выбрать в зависимо- сти от характера движения механизма, который нужно получить. Число входных звеньев должно быть равно числу степеней подвижности ме- ханизма.

В современном машиностроении широкое применение получили плоские механизмы.

Степень подвижности такого механизма определяется по формуле П.Л.Чебышева:

W = 3n – 2 p5 -1p4 ,

где    W – число степеней подвижности;

3 – число движений, которыми обладает звено на плоскости;

n – число подвижных звеньев;

p5, p4 – число кинематических пар 5-го и 4-го классов.

 

Группа начальных звеньев

В группу начальных звеньев обязательно входит стойка (станина) и входное звено.

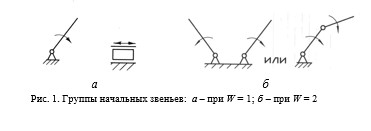
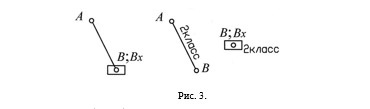
При степени подвижности механизма  W = 1 группа начальных звеньев может быть представлена в вариантах, показанных на рис. 1, а.

Если W =2, то группа начальных звеньев может быть представлена в вариантах, показанных на рис. 1,б.

а                                                      б

Рис. 1. Группы начальных звеньев: а – при W = 1; б – при W = 2

 

 

Структурная группа (группа Ассура) – кинематическая цепь, со- держащая четное число подвижных звеньев, в случае присоединения которой элементами свободных кинематических пар к стойке образует- ся система с нулевой степенью подвижности.

Для проведения структурного анализа механизма необходимо вы- делить начальную группу звеньев, а оставшуюся часть разложить на структурные группы в определенной последовательности:

а) отсоединение структурных групп начинать с наиболее удален- ных от входного звена;

б) после отсоединения первой группы продолжают отсоединять от оставшейся кинематической цепи следующую группу, проверив сте- пень подвижности оставшихся звеньев.

В результате разложения должно остаться одно входное звено, ес- ли  степень  подвижности  всего  механизма  была  равна  единице;  если

 

степень подвижности всего механизма равна двум, то должно остаться два входных звена.

 

Примечания:

1– При разделении механизма на структурные группы следует иметь в виду, что одна и та же кинематическая пара может входить только в одну структурную группу;

2– При разделении структурной группы на отдельные звенья одна и та же кинематическая пара показывается у того и другого звена, если эти звенья входили в нее в составе структурной группы.

После этого определяется класс и порядок каждой структурной группы, затем класс и порядок механизма в целом.

Класс группы определяется наивысшим классом входящего в нее контура (звена), класс контура определяется количеством кинематиче- ских пар, в которые входит.

Порядок группы определяется количеством свободных элементов кинематических пар, которыми группа присоединяется к входному зве- ну и стойке или к механизму и стойке.

Класс и порядок всего механизма определяется классом и поряд- ком наиболее сложной структурной группы, механизма, то есть наивысшим классом и наивысшим порядком группы, входящей в состав механизма.

Наиболее часто встречаются  двухповодковые группы:

 

n = 2;

p5  = 3;

W = 0.

 

 

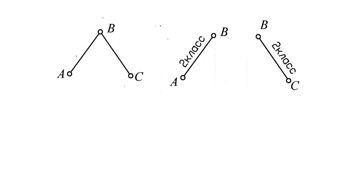
Контуры АВ и ВС – 2-го класса, так как каждый из них входит в две кинематические пары (рис. 2).

Контуры АВ и ВВХ – 2-го класса, так как каждый из них входит в две кинематические пары (рис. 3).

 

Рис. 3.

Контуры ОА/ и АА/ – 2-го класса, так как каждый из них входит в две кинематические пары (рис. 4).

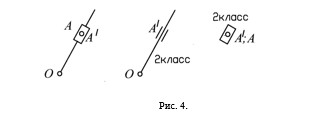
Рис. 4.

Группы (рис. 2, 3, 4) – 2-го класса второго порядка, так как каждая из них состоит из двух контуров 2-го класса и имеет по два свободных элемента кинематических пар.

Трехповодковые группы:

 

n = 4;

p5  = 6;

W = 0.

 

Контуры АВ, DЕ, СК – 2-го класса, так как каждый из них входит в две кинематические пары (рис. 5).

Контур ВDС – 3-го класса, так как входит в три кинематические пары.

Группа  3-го класса третьего порядка. Она состоит из трех конту-

 

ров 2-го класса и одного контура 3-го класса и имеет три свободных элемента кинематических пар.

 

ПРИМЕР      ВЫПОЛНЕНИЯ

Пример 1. Произвести структурный анализ рычажного механизма качающегося конвейера (рис. 6).

 

Рис. 6. Кинематическая схема: звено 1– кривошип; звено 2 – шатун; звено 3 – коромысло; звено 4 – шатун; звено 5 – ползун.

 

• Определим степень подвижности механизма (рис. 6) по фор- муле  П. Л. Чебышева.

 

где

n = 5;

p5  = 7;

W

p4  = 0.

= 3n – 2 p5 -1p4 ,

 

Все кинематические пары низшие.

Поэтому W= 3·5 – 2·7= 1, то есть в данном механизме одно входное звено ОА. Следовательно, обеспечивается структурное условие существования механизма.

 

• Разобьем механизм на структурные группы.

 

Рис. 7. Группа звеньев 4-5

n=2;   p5=3;  W=3·2 – 2·3=0.

Группа звеньев 4-5 – 2-го класса (рис. 7), так как контуры 4-5

имеют 2 класс.

Группа звеньев 4-5 – второго порядка, так как имеет два свобод- ных элемента кинематических пар (свободными элементами в точке С присоединяется к другой группе, а в точке DХ  ползуна присоединяется к неподвижной направляющей  х–х, рис. 6).

Группа звеньев 2-3 – 2-го класса (рис. 8), так как контуры АВ и О1В имеют 2-й класс. Связь контура О1В с группой 4-5 в точке С – пас- сивная, поэтому эта пара не принимается во внимание (рис.6).

 

n=2; p5=3; W=3·2 – 2·3=0.

 

Рис. 8. Группа звеньев 2-3

Группа звеньев 2-3 – второго порядка, так как имеет два свобод- ных элемента кинематических пар (свободным элементом в точке А присоединяется к входному звену, а свободным элементом в точке 01 присоединяется к стойке (рис. 8).

Вывод:  данный механизм имеет 2-й класс, второй порядок, так как в его состав входят две группы 2-го класса и  второго порядка.