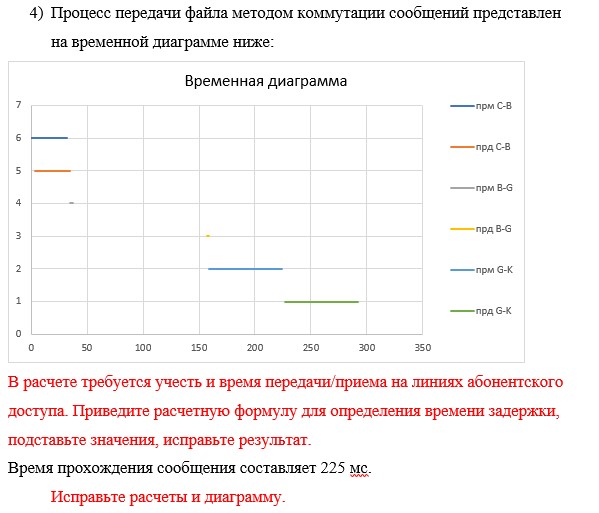
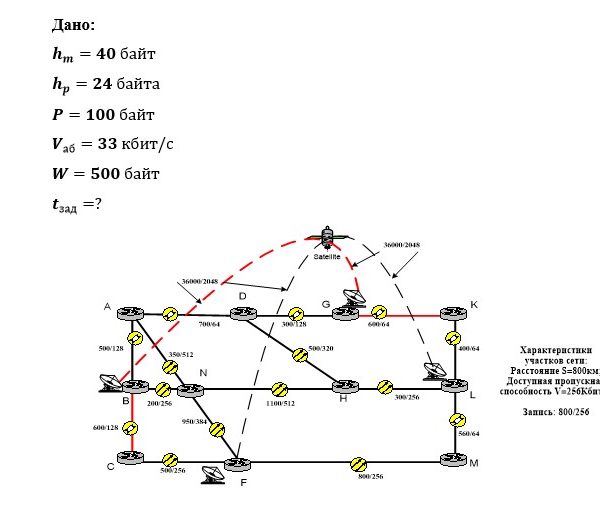
Приведите пояснения по каждой временной диаграмме.

2. Рассчитайте:
3. Скорость модуляции линейного сигнала (B, Бод) при использовании заданных линейных кодов.
4. Теоретически необходимую ширину полосы пропускания линии (∆F, Гц) для передачи сигналов в каждом случае при отсутствии шума в линии (предел Найквиста).

 Для сигнала в коде NRZ: длительность битового интервала  = 1/V равна длительности бодового интервала . Полоса частот необходимая для передачи сигнала в коде NRZ при поддержании заданной скорости передачи информации .

Дополните решение.

ЗАДАЧА 3

Приведите процедуру передачи кадров и исправления ошибок LAPB, используемую в сетевом стандарте Х.25, при взаимодействии станций на звене передачи данных в асинхронном сбалансированном режиме при следующих условиях:

• Нумерация кадров осуществляется по mod
• Окно передачи равно 2 сообщениям.
• Станция А передает 2 информационных кадра с номерами 0 – 1, станция В передает 4 информационных кадра с номерами 0 – 3.
• Станция В обнаруживает ошибку в принятом информационном кадре с номером 0, станция А обнаруживает ошибку в принятом информационном кадре с номером 2.

 

Решение

Временные диаграммы процедуры приведены в таблице ниже. Пояснения:

U, I, S – тип кадра.

Ненумерованные кадры U являются управляющими и используются в процессе установления и разъединения логического канального соединения.

Информационные кадры (ИК) I используются для передачи информации, то есть пакетов сетевого уровня. Все ИК нумеруются.

Супервизорные кадры S используются для передачи положительных или отрицательных уведомлений на принятые ИК, если на передающей его стороне нет ИК для передачи.

Переменная Vs содержит текущее значение номера ИК на передачу, увеличивается на 1 после отправки очередного ИК.

Переменная Vr содержит текущее значение ожидаемого номера ИК на прием, увеличивается на 1 после приема ИК без ошибок (OK) с номером Ns, равным значению Vr принимающей стороны.

Ns – номер передаваемого ИК, Nr – ожидаемый номер ИК на прием.

Бит опроса/окончания P/F в командном кадре обозначается P и устанавливается в «1», если требуется немедленный ответ. При передаче ИК передатчик устанавливает Р=1, когда буфер повторной передачи заполнен неподтвержденными кадрами. В кадре-ответе на полученную команду, этот бит обозначается F и устанавливается в «1».

Таймер T контролирует время получения ответа. Запуск таймера соответствует посылке P=1. После истечения таймера передатчик повторяет посылку неподтвержденных ИК.

В таблице в скобках после типа кадра указано содержимое поля управления.

 

 

 

 

 

A	Vs	Vr	CRC	Сообщение, комментарии	CRC	Vr	Vs	B
T				→ U (SABM, P=1) Станция A предлагает установить асинхронный сбалансированный режим работы. Работает таймер T контроля времени получения ответа
	0	0	OK	← U (UA, F=1) Станция B отвечает согласием	OK	0	0
После обмена ненумерованными кадрами установления режима работы на станциях A и B выделяются аппаратно-программные ресурсы для поддержания логического соединения.
	0	0		→ I (Ns=0, Nr=0, P=0) Станция A передает нулевой ИК. На ст. B в принятом кадре обнаружены ошибки.	error			Ошибка, ИК 1 стирается
Ns=Vr запись в буфер			OK	← I (Ns=0, Nr=0, P=0) Станция B передает нулевой ИК и необходимость повтора ИК 0: Nr=0. ИК 0 от станции B успешно принят станцией A		0	0
	0	1		→ I (Ns=0, Nr=1, P=0) Станция A передает ИК 0 и подтверждение приема ИК 0 (Nr=1, т.е. ст. A ждет ИК с номером 1). На ст. B ИК 1 принят успешно.	OK			Ns=Vr запись в буфер
Ns=Vr запись в буфер			OK	← I (Ns=1, Nr=1, P=0) Станция B передает ИК 1 и подтверждает прием ИК 0: Nr=1. На ст. A ИК 1 принят успешно.		1	1
T	1	2		→ I (Ns=1, Nr=2, P=1) Станция A передает ИК 1 и подтверждает прием ИК 1 от ст. B. Поскольку cт. A передавать больше нечего, ст. B требует передать подтверждение приема (P=1). Работает таймер T получения ответа. На ст. B ИК 1 принят успешно.	OK			Ns=Vr запись в буфер
Ошибка, ИК 2 стирается			error	← I (Ns=2, Nr=2, P=0) Станция B передает ИК 2 и подтверждение приема ИК 1: Nr=2. На ст. A в принятом кадре обнаружены ошибки.		2	2
			ignore	← I (Ns=3, Nr=2, P=1) Станция B передает ИК 3. Поскольку cт. B передавать больше нечего, ст. B требует передать подтверждение приема (P=1). Работает таймер T получения ответа. На ст. A кадр игнорируется, т.к. ранее были обнаружены ошибки в ИК2.		2	3	T
	2	2		→ S (REJ, Nr=2, F=1) На станции A ИК закончились. Поэтому ст. A передает уведомление о необходимости повторной передачи ИК 2 в супервизорном кадре.	OK
Ns=Vr запись в буфер			OK	← I (Ns=2, Nr=2, P=0) Станция B повторяет передачу ИК 2. На ст. A ИК 2 принят успешно.
Ns=Vr запись в буфер	2	3	OK	← I (Ns=3, Nr=2, P=1) Ст. B передает ИК 3. Поскольку cт. B передавать больше нечего, ст. B требует передать подтверждение приема (P=1). Работает таймер T получения ответа. На ст. A ИК 3 принят успешно.		2	3	T
	2	4		→ S (RR, Nr=4, F=1) Станция A передает подтверждение приема ИК 3 в супервизорном кадре. Внесите изменения в процедуру, если при приеме супервизорного кадра будут обнаружены ошибки.	ERROR
				← U (DISC, P=1) Станция B предлагает разъединить данное логическое соединение, так как у нее больше нет кадров для передачи. Работает таймер T получения ответа.		2	4	T
	3	5		→ U (UA, F=1) Станция A отвечает согласием.

Дополните решение задачи.

 

ЗАДАЧА 4

Система передачи данных использует циклический код с параметрами (7,4) с образующим полиномом g(x) = x³ + x² + 1. На вход кодера канала поступает информационная последовательность u = 0110.

1. Запишите образующую матрицу G заданного кода в каноническом виде. Определите кодовое расстояние кода d₀ (d_min).
2. Определите кодовую комбинацию v на выходе кодера.
3. Внесите двойную ошибку (t=2) в любые разряды комбинации v. Вы получили искаженную комбинацию y на входе декодера канала в приемной части.
4. Определите синдром s комбинации y.
5. Ответьте на вопросы:
   1. Декодер обнаружил ошибки? (Да, нет, почему?)
   2. Декодер способен исправить обнаруженные ошибки?

 

Решение

 

1. Запишем образующую матрицу заданного кода G, используя заданный образующий полином g(x).

Преобразуем полученную матрицу к каноническому виду. Для этого записываем строки матрицы G в обратном порядке, а затем при помощи сложения строк по модулю 2 приводим к каноническому виду. Получаем:

Минимальный вес кодового слова в образующей матрице G_кан t = 3. Следовательно, кодовое расстояние заданного кода d₀ = 3.

2. Задана информационная последовательность U = 0110. Кодовая комбинация V на выходе кодера может быть найдена как произведение
   V = U×G_кан,

или можно вычислить проверочные разряды кодовой комбинации через образующий полином g(x). Воспользуемся вторым способом.

R(x) = [U(x)×x^n–k]mod g(x) =[(x²+ x¹)×x³]mod(x³+ x²+1) = x² → 100

Выполним деление в двоичном виде

0	1	1	0	0	0	0	1	1	0	1
	1	1	0	1			1	0	0
				1	0	0

 

V = 0110 100

Для проверки разделим полученную комбинацию на заданный образующий полином:

0	1	1	0	1	0	0	1	1	0	1
	1	1	0	1			1	0	0
				0	0	0

 

Полученная комбинация делится на образующий полином без остатка, и, следовательно, является разрешенной комбинацией заданного кода.

3. По заданию при передаче по дискретному каналу возникла комбинация ошибок весом t = 2. Пусть вектор ошибки имеет вид (выбираем произвольно) e = 0011. Вектор (комбинация) ошибки имеет длину, равную длине передаваемых комбинаций кода. Исправьте е. Тогда на входе декодера приемника появляется комбинация
   Y = VÅe = 0101 100,

как результат поразрядного сложения комбинаций по модулю 2.

4. Декодер циклического кода вычисляет синдром принятой последовательности S(x) = Y(x)mod g(x). Разделим принятую последовательность Y на образующий полином и найдем остаток от деления.

0	1	0	1	1	0	0	1	1	0	1
	1	1	0	1			1	0	0
		1	1	0	0
		1	1	0	1
					1	0

Очевидно, S = 010 ≠ 0.

5. Синдром не равен нулю, следовательно, декодер установил наличие ошибок в принятой комбинации.

Определим кратность ошибки, которую может исправить данный код. Число проверочных символов (n–k) = 3, следовательно, имеем 2³ = 8 синдромов.

1 синдром, S = 000, соответствует отсутствию ошибок;

7 синдромов соответствуют наличию одиночных ошибок, т.к. одиночная ошибка может появиться в n = 7 позициях.

1+7 = 8.

Т.е. данный код не способен исправлять ошибки кратности t = 2, только t = 1. Произойдет ошибочное исправление одиночной ошибки.

Уточните ответ. Поясните, какой именно бит принятой комбинации будет исправлен декодером, и какая комбинация будет выдана получателю сообщения. Только тогда мы убедимся, что произошло ошибочное декодирование.

Вывод. Выбранная комбинация ошибок не будет исправлена.