Лабораторная работа № 4.4 (27)

 

ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА

С ПОМОЩЬЮ ЭЛЕКТРОННО-ЛУЧЕВОЙ ТРУБКИ

Цель работы:  изучение закономерностей движения заряженных частиц в электрическом и магнитном полях; определение скорости и удельного заряда электрона.

ТЕОРЕТИЧЕСКИЙ  МИНИМУМ

Сила Лоренца

На заряд q, движущийся со скоростью  в электромагнитном поле, действует сила Лоренца

 

Направление магнитной составляющей определяется правилом векторного произведения и знаком заряда: для положительного заряда ( ) правую тройку векторов образуют векторы ,  и (рис. 1), для отрицательного заряда ( ) – векторы ,  и . Направление магнитной составляющей силы Лоренца можно определить и с помощью правила левой руки.

 

Правило левой руки: расположите ладонь левой руки так, чтобы в нее входил вектор , а четыре пальца направьте вдоль вектора , тогда отогнутый на 90° большой палец покажет направление силы , действующей на положительный заряд. В случае отрицательного заряда направление вектора  противоположно. В любом случае вектор  перпендикулярен плоскости, в которой лежат векторы  и .

 

Движение заряженных частиц в магнитном поле

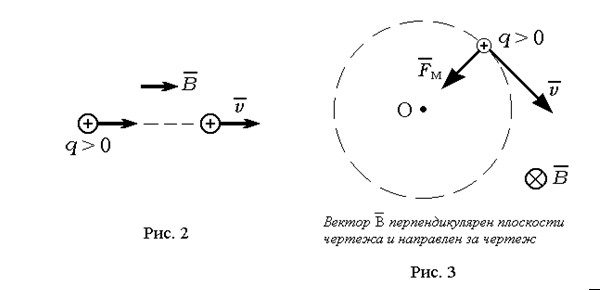
Если частица движется вдоль линии магнитной индукции (  или ), то . Тогда согласно выражению (4) . В этом случае магнитное поле не влияет на движение заряженной частицы (рис. 2).

Если заряженная частица движется перпендикулярно линиям магнитной индукции , то . Тогда согласно (4) . Так как вектор этой силы всегда перпендикулярен вектору скорости  частицы, то сила  создает только нормальное (центростремительное) ускорение , при этом скорость заряженной частицы изменяется только по направлению, не изменяясь по модулю. Частица в этом случае равномерно движется по дуге окружности, плоскость которой перпендикулярна линиям индукции (рис. 3).

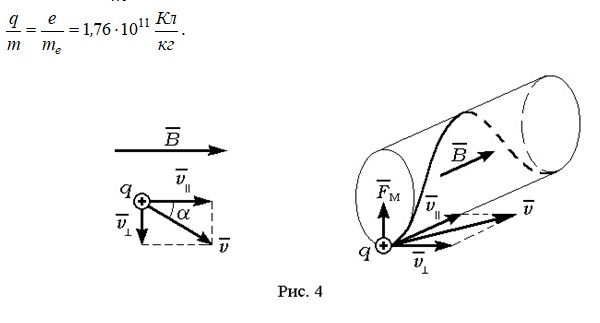
Если вектор скорости  заряженной частицы составляет с вектором  угол , то магнитная составляющая силы Лоренца будет определяться согласно (3), а модуль согласно выражению (4). В этом случае частица участвует одновременно в двух движениях: поступательном с постоянной скоростью  и равномерном вращении по окружности со скоростью . В результате траектория заряженной частицы имеет форму винтовой линии (рис. 4).

Удельный заряд частицы

Удельный заряд частицы – это отношение заряда q частицы к ее массе m. Величина – важная характеристика заряженной частицы. Для электрона .

МЕТОДИКА ЭКСПЕРИМЕНТА

 

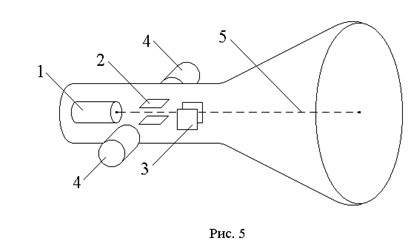
В работе изучается движение электронов в однородных электрическом и магнитном полях. Источником электронов является электронная пушка 1 электроннолучевой трубки осциллографа[1] (рис. 5). Электрическое поле создается между парой вертикально отклоняющих пластин 2 электронно-лучевой трубки при подаче на них напряжения U. (Горизонтально отклоняющие пластины 3 в работе не используются.) Напряженность  электрического поля направлена вертикально.

Магнитное поле создается двумя катушками 4, симметрично расположенными вне электроннолучевой трубки, при пропускании по ним электрического тока. Вектор магнитной индукции  направлен горизонтально и перпендикулярно оси трубки.

В отсутствии электрического и магнитного полей электроны движутся вдоль оси трубки со скоростью , при этом светящееся пятно находится в центре экрана. При подаче напряжения U на пластины 2 между ними создается электрическое поле, напряженность которого  перпендикулярно вектору начальной скорости электронов. В результате пятно смещается. Величину y этого смещения можно измерить, воспользовавшись шкалой на экране осциллографа.

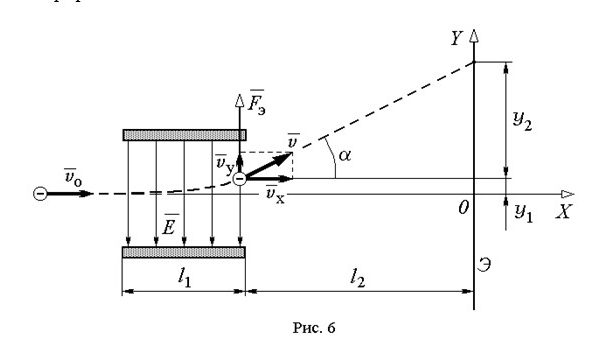
Однако в электрическом поле на электрон действует согласно (2) электрическая составляющая силы Лоренца

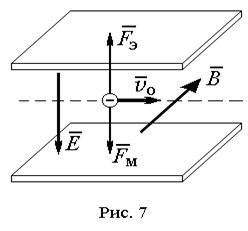
Если по катушкам 4 (рис. 5) пропустить электрический ток, то на пути электронов возникнет магнитное поле. Изменяя силу тока I в катушках, можно подобрать такую величину и направление магнитной индукции , что магнитная составляющая силы Лоренца  скомпенсирует электрическую составляющую . В этом случае пятно снова окажется в центре экрана. Это будет при условии равенства нулю силы Лоренца

или   .

Как видно из рис. 7, это условие выполняется, если вектор магнитной индукции  перпендикулярен векторам  и , что реализовано в установке. Из этого условия можно определить скорость электронов

.                                                     (7)

Поскольку практически измеряется напряжение U, приложенное к пластинам, и расстояние d между ними, то пренебрегая краевыми эффектами можно считать, что , тогда

.                                                   (8)

Измеряя смещение у электронного пучка, вызванное электрическим полем  Е, а затем подбирая такое магнитное поле В, чтобы смещение стало равным нулю, можно из уравнений (6) и (8) определить удельный заряд электрона

.                                          (9)

Схема установки показана на рис. 8. Электроннолучевая трубка расположена в корпусе осциллографа 1, на передней панели которого находится экран трубки 2 и две пары клемм. Клеммы ПЛАСТИНЫ соединены с вертикально отклоняющими пластинами трубки. Клеммы КАТУШКИ соединены с катушками 4 электромагнита, создающего магнитное поле. (Расположение катушек видно через прозрачную боковую стенку осциллографа.)

Выпрямитель 5 и блок 6 служат для создания, регулировки и измерения постоянного напряжения на управляющих пластинах трубки и постоянного тока через катушки электромагнита. Переключатель  позволяет изменить полярность напряжения на пластинах, а переключатель – направление тока через катушки электромагнита.

Параметры установки: d = 7,0 мм; = 25,0 мм; = 250 мм.

 

Приборы и принадлежности: осциллограф с электроннолучевой трубкой; выпрямитель; блок коммутации с электроизмерительными приборами.

 

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

 

1. Заполните табл. 1 характеристики электроизмерительных приборов.

 

Таблица 1

 

Наименование прибора	Система прибора	Предел измерения	Цена деления	Класс точности	Приборная погрешность
Вольтметр	Магнито-электричес-кая	50 В	1 В	1,5	= 0,75 В
Миллиамперметр	Магнито-электричес-кая	100 мА	2 мА	2,5	= 2,5 мА

 

2. Тумблером 3 (рис. 8) включите осциллограф. Ручками ЯРКОСТЬ и ФОКУС, расположенными на верхней панели осциллографа, добейтесь четкости пятна на экране. Ручкой установите пятно в центр экрана.
3. Тумблером К  включите выпрямитель. Ручками  и  установите нулевые показания вольтметра и миллиамперметра.
4. Условия проведения эксперимента (значения напряжения  на пластинах) задаются преподавателем или вариант индивидуального занятия.
5. Ручкой  установите нужное напряжение на пластинах и измерьте смещение  луча от центра экрана. Результат измерения в зависимости от направления смещения («вверх» или «вниз») запишите в табл. 2.
6. С помощью ручки и переключателя  подберите такой ток  I₁  в катушках, чтобы пятно вернулось в центр экрана. Значение силы тока запишите в табл. 2.
7. Измерения, указанные в пункте 5 и 6, проведите при двух других значениях напряжения .
8. Тумблером  измените полярность напряжения на пластинах и повторите измерения, указанные в пунктах 5, 6 и 7.

Таблица 2

U, В	вверх, мм	вниз, мм	, мм	, мА	, мА	, мА	, мТл	, м/с	e/m, Кл/кг
10	3	6	4,5	10	14	12	0,068	2,10·107	2,12·1011
20	7	11	9	22	26	24	0,137
40	17	18	17,5	46	49	47,5	0,268

9. По приложенному к установке градуировочному графику электромагнита и по среднему значению силы тока в каждом испытании определите значения магнитной индукции В и занесите их в табл. 2.
10. По формуле (8) рассчитайте скорость электронов в каждом опыте и среднее значение по всем испытаниям.

=2,11·10⁷ м/с

11. Используя формулу , рассчитайте анодное напряжение в электронной пушке.
12. По формуле (9) рассчитайте значение удельного заряда электрона в каждом опыте и среднее значение по всем испытаниям.

= 2,11·10¹¹ Кл/кг

 

13. По результатам одного из опытов рассчитайте абсолютную погрешность удельного заряда электрона.

Относительные частные погрешности рассчитайте по формулам

В качестве  используйте приборную погрешность шкалы на экране осциллографа, в качестве  – приборную погрешность вольтметра. Погрешность  определяется по градуировочному графику по величине .

.

=2,11·10¹¹·0,34=0,72·10¹¹(Кл/кг).

Запишите в отчет полученный доверительный интервал величины .

=(2,11+0,72)·10¹¹ Кл/кг

 

15. В выводах

• укажите, что наблюдалось в работе;
• сравните полученное и табличное значения ; согласие считается хорошим, если табличное значение попадает в найденный доверительный интервал;
• укажите, измерение какой величины внесло основной вклад в погрешность величины .

 

Вывод: наблюдали движение электронов в скрещенных электрическом и магнитном полях с помощью электронно-лучевой трубки; измерили удельный заряд электрона =(2,11+0,72)·10¹¹ Кл/кг ; табличное значение   попадает в полученный доверительный интервал; основной вклад в погрешность измерения удельного заряда внесла ошибка измерения смещения  луча от центра экрана.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

 

1. Сила Лоренца. Направление ее составляющих.
2. Зависит ли от знака заряда сила, действующая на него со стороны:

а) электрического поля; б) магнитного поля?

3. Зависит ли от скорости и направления движения заряда сила, действующая на него:

а) в электрическом поле;

б) в магнитном поле?

4. Как движется электрон:

а) в поле между пластинами;

б) слева от пластин;

в) справа от пластин?

5. Отличается ли скорость электрона до и после пластин?
6. Как изменится смещение пятна на экране, если

а) скорость электронов увеличить вдвое;

б) анодное напряжение увеличить вдвое?

7. Изменяется ли при движении заряда в однородном магнитном поле:

а) направление скорости;

б) величина скорости?

8. Каким должно быть взаимное расположение однородных электрического и магнитного полей, чтобы электрон мог двигаться в них с постоянной скоростью? При каком условии возможно такое движение?
9. Какую роль в электронной пушке играют катод, модулятор, аноды?
10. Какую роль в электроннолучевой трубке играют:

а) электронная пушка;

б) отклоняющие пластины;

в) экран?

11. Как в установке создаются однородные поля:

а) электрическое;

б) магнитное?

12. Как изменяется смешение пятна на экране при изменении направления тока в катушках?

 

 

 

Лабораторная работа № 5.6 (32)

 

ИССЛЕДОВАНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ И РЕЗОНАНСА

В ЭЛЕКТРИЧЕСКОМ КОЛЕБАТЕЛЬНОМ КОНТУРЕ

 

Цель работы: изучение закономерностей вынужденных колебаний; определение резонансных кривых и измерение параметров контура.

 

ТЕОРЕТИЧЕСКИЙ МИНИМУМ

 

Колебания и их основные характеристики

 

Колебаниями называются процессы (движение или изменение состояния), повторяющиеся с течением времени.

Если все состояния системы последовательно повторяются через определенные равные промежутки времени, то колебания носят периодический характер. Наименьшее время T повторения одинаковых состояний называется периодом. За период T система совершает одно полное колебание. Если за время t система совершает n полных колебаний, то период T = t / n. Число полных колебаний системы, совершаемых за единицу времени, называется частотой колебаний

.                                               (1)

Подобные процессы протекают под действием возвращающей силы F, которая чаще всего прямо пропорциональна отклонению состояния системы от равновесного состояния. В линейном однокоординатном случае справедливо соотношение

,                                                  (2)

где  F – упругая или квазиупругая сила; x – отклонение системы от равновесного состояния; k – некоторый коэффициент пропорциональности, определяемый физикой колебательного процесса.

Согласно основному закону динамики поступательного движения уравнение (2) принимает вид

или   ,                       (3)

где  – циклическая частота, равная числу полных колебаний, совершаемых за  секунд. С учетом (1) циклическую частоту можно связать с периодом колебаний

.

Решение дифференциального уравнения (3) называется уравнением гармонических колебаний

,                                      (4)

где     – значение колеблющейся величины  в момент времени ;

– амплитуда колебаний, т.е. максимальное значение колеблющейся величины (амплитуду часто обозначают символом А);

–  фаза колебаний, которая определяет состояние системы в любой момент времени t;

– начальная фаза, т.е. значение  в момент времени t = 0.

 

Колебания, совершающиеся по закону (4) (вместо синуса может быть косинус), называются гармоническими. Система, совершающая гармонические колебания, является гармоническим осциллятором. На рис. 1 показан график гармонических колебаний (4), где по оси абсцисс отложено время t и фаза  колебаний. Различие между началом отсчета времени (t = 0) и началом отсчета фазы ( = 0) характеризуется начальной фазой .

 

Собственные колебания в электрическом колебательном контуре

Электрический колебательный контур состоит из последовательно соединенных емкости  и индуктивности  (рис. 1). Если зарядить конденсатор, а затем замкнуть ключ , то конденсатор начинает разряжаться и в контуре появляется нарастающий ток, а в катушке пропорциональное ему магнитное поле. Изменение магнитного поля приводит к появлению ЭДС самоиндукции, которая замедляет скорость разрядки конденсатора. После того, как конденсатор разрядится, и ток в контуре начнет уменьшаться, ЭДС самоиндукции будет поддерживать ток в прежнем направлении до тех пор, пока конденсатор не перезарядится. Затем следует процесс разрядки конденсатора, но в противоположном направлении. Эти процессы повторяются снова и снова, т.е. в контуре возникают собственные (свободные) колебания заряда в конденсаторе и силы тока в катушке.

Уравнение колебаний заряда  в электрическом колебательном контуре можно получить, используя закон Ома для замкнутой цепи: сумма напряжений равна действующей в цепи ЭДС. Для данного случая напряжение на конденсаторе равно ЭДС самоиндукции . Так как ,  и , то . Отсюда получаем дифференциальное уравнение

.                                     (1)

Решением этого уравнения является гармоническая функция

,                              (2)

где собственная частота колебаний определяется выражением

.                                             (3)

 

Таким образом, величина заряда  конденсатора с течением времени изменяется по гармоническому закону (2). График зависимости  показан на рис. 2, где по оси абсцисс отложено и время , и фаза  колебаний. Различие между началом отсчета времени ( ) и началом отсчета фазы ( ) определяется начальной фазой .

 

 

Затухающие колебания и их характеристики

Любой реальный колебательный контур имеет некоторое активное сопротивление  (рис. 3). Поэтому часть энергии электромагнитных колебаний превращается в тепло, вследствие чего амплитуда колебаний в контуре постепенно уменьшается, колебания затухают.

Закон Ома для рассматриваемого случая имеет вид . Как и для незатухающих колебаний ,  и , а напряжение на активном сопротивлении . Тогда . Отсюда получаем дифференциальное уравнение затухающих колебаний

или             .

Решением этого уравнения является функция

,                                        (4)

где     – начальная амплитуда колебаний (в момент времени );

– коэффициент затухания;

– циклическая частота затухающих колебаний;

– как и выше, частота собственных незатухающих колебаний.

График затухающих колебаний показан на рис. 4, а. С увеличением активного сопротивления  затухание колебаний происходит быстрее. При достаточно большом сопротивлении  колебания вообще не возникают – наблюдается апериодический разряд конденсатора (рис. 4, б). Активное сопротивление, при котором периодические колебания переходят в апериодический процесс, называется критическим сопротивлением .

Пока , частота  имеет действительное значение, что соответствует периодическому процессу (рис. 4, а). При  периодический процесс переходит в апериодический (рис. 4, б). Приравнивая правые части уравнений для  и , получаем выражение для критического сопротивления

.                                         (5)

Огибающая колебаний, показанная на рис. 4, а пунктирной линией, отражает изменение амплитуды с течением времени, происходящее по закону

.                                         (6)

Отсюда следует физический смысл коэффициента затухания : за время  амплитуда уменьшается в е раз (е– основание натурального логарифма).

Уменьшение амплитуды за время одного полного колебания, то есть за период, характеризует логарифмический декремент

,                                       (7)

где  и  – амплитуды, соответствующие моментам времени t и (t+T), то есть отличающимся на период (рис. 4, а).

Так как напряжение на конденсаторе пропорционально его заряду, то колебания напряжения и заряда конденсатора происходят в одинаковой фазе. Закон колебаний напряжения и заряда аналогичны

.                           (8)

Колебания силы тока в контуре

(9)

сдвинуты по фазе на величину  по сравнению с колебаниями напряжения  на конденсаторе, но совпадают по фазе с колебаниями напряжения на активном сопротивлении R

.                    (10)

Значение  лежит в пределах , зависит от параметров контура и определяется выражением

.                                       (11)

 

Вынужденные колебания в электрическом колебательном контуре

Для возбуждения вынужденных колебаний в электрическом колеба-тельном контуре необходимо его подключение к источнику тока, ЭДС E которого периодически изменяется с течением времени (рис. 1).

Рассмотрим случай гармонического изменения ЭДС:  . По закону Ома сумма напряжений на элементах R  и C равна суммарной ЭДС, действующей в контуре

,                                       (1)

где I – сила тока в контуре; q – заряд конденсатора. По определению .

С учетом этого, после дифференцирования уравнения (1) по времени, получаем дифференциальное уравнение вынужденных колебаний силы тока в колебательном контуре

  ,                                   (2)

где   коэффициент затухания, а   – собственная частота колебаний, зависящие от параметров контура. Решение дифференциального уравнения (2), соответствующее установившимся колебаниям, называется уравнением вынужденных колебаний в колебательном контуре и имеет вид

.                                          (3)

Как видим, ток в контуре изменяется по гармоническому закону с той же частотой , как и внешняя ЭДС, а амплитуда I₀ силы тока зависит от частоты  внешней ЭДС и параметров контура

.                                      (4)

Рис.2

Зависимость амплитуды I₀ колебаний от частоты  внешней ЭДС называется резонансной кривой. На рис. 2 показаны резонансные кривые для силы тока в контуре при различных значениях сопротивления  контура. Видим, чем меньше R, тем больше амплитуда тока при резонансе и тем острее резонансная кривая.

Важнейшим свойством резонансной кривой является существование максимума амплитуды колебаний при некоторой частоте, которая называется резонансной. В колебательном контуре амплитуда силы тока (4) достигает максимального значения при условии , следовательно, резонансная частота для силы тока

.                                        (5)

Таким образом, резонансная частота колебаний электрического тока в контуре совпадает по величине с собственной частотой колебаний в колебательном контуре и не зависит от значения активного сопротивления R контура.

 

МЕТОДИКА ЭКСПЕРИМЕНТА

 

Конденсатор, катушка индуктивности, активное сопротивление и источник переменной ЭДС, соединенные последовательно, образуют колебательный контур, в котором происходят вынужденные колебания.

Схема установки изображена на рис. 3. Конденсаторы с известной  и неизвестной  емкостью, катушки с известной  и неизвестной  индуктивностью и миллиамперметр для измерения силы тока в контуре смонтированы в лабораторном стенде и их выводы расположены на лицевой панели. Включение в цепь известных или неизвестных ёмкости или индуктивности производится соответствующими переключателями на стенде.

Активное сопротивление  контура задается магазином сопротивлений.

 

Источником переменной ЭДС служит генератор, создающий гармонические колебания напряжения. Частота колебаний  устанавливается соотвествующими клавишами генератора, ручкой FREQUENCY (частота) и показывается на индикаторе. Амплитуда напряжения на выходе генератора регулируется ручкой AMPL.

Амплитуда колебаний силы тока в контуре измеряется миллиамперметром .

Если в контуре один из параметров (L или С) неизвестен, то определяют резонансную частоту  и, используя (5), из соотношения

(6)

вычисляют неизвестную величину. Таким образом, установка может быть использована для определения неизвестной емкости  или неизвестной индуктивности .

 

Приборы и принадлежности: лабораторный стенд; генератор; магазин сопротивлений.

 

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

 

1. Объем работы и условия проведения опыта устанавливаются преподавателем или вариантом индивидуального задания.
2. Заполните табл.1 характеристик миллиамперметра.

Таблица 1

Наименование прибора	Система прибора	Предел измерения	Цена деления	Класс точности	Приборная погрешность
Миллиамперметр для измерения силы тока в контуре	Магнито-электричес-кая	5 мА	0,1 мА	1,5	0,03 мА

 

3. Переключателями на стенде включите в контур известные емкость и индуктивность C = 0,03 мкФ, L = 12,3 мГн.
4. По формуле (6) рассчитайте теоретическое значение . Значения L и С указаны на установке.
5. Включите генератор и установите частоту, равную полученному значению . Ручкой AMPL генератора установите силу тока в контуре примерно равной 2/3 предела измерения миллиамперметра и в дальнейшем при снятии резонансной кривой не изменяйте амплитуду сигнала на выходе генератора.
6. Изменяя с помощью ручки FREQUENCY частоту генератора в одну и в другую сторону от частоты , проследите качественно на шкале миллиамперметра за изменением амплитуды колебаний в контуре. Результаты наблюдений запишите в отчет.
7. При двух заданных значениях сопротивления и  магазина измерьте резонансные кривые контура. Каждая кривая должна содержать не менее 8-10 значений частоты в интервале от 1 кГц до 20 кГц. Особенно подробно следует определять силу тока в контуре в области резонансной частоты . Результаты измерений занесите в табл. 2.

Таблица 2

R1 = 50 Ом		R2 = 150 Ом
, кГц	I, мкА	, кГц	I, мкА
3	0,2	4,5	0,1
5,5	0,3	5,5	0,3
6	0,6	6	0,5
6,4	1,0	7	1,6
7	2,1	8	2,5
7,5	3,5	9	2,3
8	4,8	10	1,6
9	3,4	11	1,1
10	2,1	12	0,8
12	0,9	13	0,7
14	0,5	14	0,5
15	0,4	15	0,4

 

8. Постройте на одном графике обе резонансные кривые, откладывая по оси абсцисс частоту , а по оси ординат – силу тока I.

На каждой кривой укажите активное сопротивление контура, которое складывается из сопротивления магазина R и сопротивления катушки , значение которого указано на установке. Обсудите зависимость  и формы резонансной кривой от сопротивления контура.

Образец графика

 

9. Включите в контур неизвестную индуктивность вместо известной. По максимуму тока в контуре определите  и по формуле (6) вычислите величину .

=1200 Гц

10. Измерьте неизвестную емкость . Для этого включите в контур известную индуктивность и неизвестную емкость . По максимуму тока в контуре определите  и по формуле (6) вычислите неизвестную .

= 4200 Гц

Вывод: Исследовали вынужденные колебания в электрическом колебательном контуре; определили резонансные кривые; убедились в том, что величина сопротивления ________ на резонансную частоту и __________на амплитуду тока при резонансе – чем __________ сопротивление, тем ________амплитуда тока при резонансе и _________ резонансная кривая; экспериментальное значение резонансной частоты __________ с теоретическим; используя явление резонанса, определили неизвестную емкость и индуктивность

=  _______  мкФ, =   _______ Гн.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

 

1. Нарисуйте принципиальную схему колебательного контура, в котором происходят вынужденные колебания. Назовите параметры контура. Как зависят от параметров контура коэффициент затухания и частота собственных колебаний?
2. Запишите дифференциальное уравнение вынужденных колебаний силы тока в контуре в случае гармонического изменения ЭДС. Согласно какому закону это уравнение записано?
3. Найдите решение дифференциального уравнения вынужденных колебаний силы тока в контуре в случае гармонического изменения ЭДС, соответствующее колебаниям, устанавливающимся в контуре. С какой частотой происходят колебания силы тока в контуре?
4. Что такое резонансная кривая? От чего зависит острота максимума?
5. В чем заключается явление резонанса? При каком условии он происходит?
6. Как зависит резонансная частота от параметров контура R, L, С?
7. Как в работе находится неизвестная емкость или неизвестная индуктивность? Зависит ли результат от величины сопротивления?
8. Из чего складывается активное сопротивление контура?
9. Как и в каких пределах изменяется частота генератора?
10. Что называется полным сопротивлением цепи? Чему оно равно при резонансе?
11. Зависимость силы тока в контуре от времени имеет вид . Какими параметрами контура определяется частота и амплитуда I₀ ?

 

 

Лабораторная работа № 5.9 (35, 35м)

ИНТЕРФЕРЕНЦИЯ СВЕТА НА ПЛОСКОПАРАЛЛЕЛЬНОЙ ПЛАСТИНЕ

Цель работы: изучение явления интерференции света; определение показателя преломления стекла с помощью полос равного наклона.

ТЕОРЕТИЧЕСКИЙ МИНИМУМ

Свет – это электромагнитная волна, т.е. распространяющееся в пространстве переменное электромагнитное поле. Колебание напряженностей электрического  и магнитного  полей, характеризующих электромагнитную волну, происходит перпендикулярно вектору скорости  волны (направлению луча) во взаимно перпендикулярных плоскостях, так что векторы ,  и  образуют правую тройку векторов. На рис. 1 показана мгновенная «фотография» электромагнитной волны, распространяющейся вдоль оси . Стрелками на рисунке показаны векторы  и . С течением времени изображенная картина движется вдоль луча со скоростью .

Если заданы направление вектора  и направление одного из векторов, например , то направление другого ( ) определяется однозначно. Поэтому, описывая электромагнитную (световую) волну, принято указывать лишь направление колебаний электрического вектора , и это направление называют направлением колебаний световой волны (светового вектора). Заметим, что именно электрическое поле оказывает гораздо более сильное воздействие на электроны вещества, чем магнитное поле.

Интерференция света представляет собой сложение в пространстве двух или нескольких волн, в результате которого происходит усиление или ослабление колебаний. В тех точках пространства, в которых волны встречаются в одинаковой фазе, колебания происходят с наибольшей амплитудой, здесь наблюдается максимум (светлое пятно). Там, где волны встречаются в противофазе, наблюдается минимум (темное пятно).

Чередование темных и светлых участков, наблюдаемое на экране, фотопластинке и т.д., называется интерференционной картиной.

При интерференции не нарушается закон сохранения энергии. В среде без поглощения энергия складывающихся волн лишь перераспределяется в пространстве: в точках минимума энергия уменьшается, а в точках максимума увеличивается, но интегральная энергия по всему объему волны не изменяется.

Необходимым условием интерференции света является согласованность колебаний – когерентность волн. Волны когерентны, если у них одинаковая частота колебаний, а их векторы  колеблются в одном или близких направлениях (т.е. имеют одинаковую или близкую поляризацию). Чтобы интерференционная картина была устойчива во времени, необходимо, чтобы разность фаз двух складывающихся волн не изменялась с течением времени.

Независимые источники света не могут быть когерентными, ибо в каждом из них свет испускается множеством атомов несогласованно. Разность фаз колебаний, испускаемых атомами таких источников, беспорядочно изменяется во времени. Однако наблюдение интерференции света обычных источников все-таки возможно, если с помощью какой-либо оптической системы разделить одну волну на две или несколько волн и сдвинуть их относительно друг друга.

На практике особенно легко получить интерференционную картину для света лазера, излучение которого обладает высокой монохроматичностью и большой длиной когерентности. Длиной когерентности называется наибольшее расстояние вдоль распространения волны, на котором колебания еще можно считать когерентными между собой.

Рассмотрим две когерентные волны, полученные путем разделения некоторой исходной световой волны. После разделения волны проходят различные пути до точки наблюдения, при этом их оптическая разность хода

,

где  и  – оптические пути, проходимые первой и второй волнами. Для однородной среды оптический путь

,                                                         (1)

где  – геометрический путь;  – показатель преломления среды, равный отношению скорости света  в вакууме к скорости света  в данном веществе

.                                                    (2)

Так как всегда , то . Величина   зависит от длины волны света и свойств вещества.

Из выражений (1) и (2) следует, что оптический путь – это расстояние, которое прошел бы свет в вакууме за то же время.

Если оптическая разность хода равна целому числу длин волн

( ),                                 (3)

то разность фаз складываемых волн равна  , и колебания, возбуждаемые обеими волнами в точке наблюдения, находятся в одинаковой фазе. Следовательно, выражение (3) является условием интерференционного максимума.

Если оптическая разность хода равна нечетному числу длин полуволн

( ),                             (4)

то разность фаз складываемых волн будет равна  и колебания, возбуждаемые обеими волнами в той же точке, находятся в противофазах. Следовательно, формула (5) является условием интерференционного минимума.

МЕТОДИКА ЭКСПЕРИМЕНТА

 

В данной работе исследуется интерференция при отражении лазерного света от плоскопараллельной стеклянной пластины. Проведя соответствующие измерения, можно определить показатель преломления стекла.

Принципиальная оптическая схема установки показана на рис. 2. Параллельный пучок света от лазера 1 проходит через линзу 2, задний фокус О которой расположен в плоскости экрана 3. Выйдя из отверстия в экране, расходящийся пучок света падает на стеклянную пластину 4. При этом часть света отражается от передней, а часть – от задней поверхностей пластины. Таким образом, осуществляется разделение исходного лазерного пучка на две когерентные волны. Встречаясь на экране, эти волны интерферируют между собой, и в результате образуется система концентрических светлых и темных колец с общим центром в точке О. Такая картина носит название полос равного наклона, так как в пределах каждого кольца условие интерференции реализуется для какого-то одного значения угла  падения света на пластину.

Необходимая для интерференции разность фаз колебаний возникает вследствие того, что волны проходят разные оптические пути: одна из волн часть пути проходит в стеклянной пластинке с показателем преломления , а другая – в воздухе, показатель преломления которого считаем равным единице. В итоге разность хода двух интерферирующих волн

,                                          (5)

где  – толщина пластинки;  – угол падения лучей на пластину[2].

Используя условие (4) минимума интерференции, из выражения (5) получим условие наблюдения темных колец

,                                          (6)

где целые числа  называются порядком интерференции. Для соседних темных колец величина  отличается на единицу.

Из рис. 2 следует, что радиус -го темного кольца на экране

,                                             (7)

где  – расстояние от экрана до пластины.

В условиях данного опыта ,  и угол  мал, поэтому можно считать, что   и тогда соотношение (6) можно записать в виде

.                                         (8)

На основании выражений (7) и (8) получим

.                                        (9)

Из формулы (9) видим, что величина  линейно зависит от порядка интерференции . Поэтому, если построить график зависимости  от , то угловой коэффициент  полученной прямой дает возможность определить множитель при  в уравнении (9)

.                                                   (10)

Если известны величины ,  и длина волны , то из формулы (10) можно определить показатель преломления  материала пластины

.                                                  (11)

Большая длина когерентности лазерного излучения позволяет получить интерференцию при большой разности хода лучей, т.е. с использованием достаточно толстой пластины. В обычном же свете интерференция наблюдается только на очень тонких пленках (например, на мыльной пленке, на пленках маслянистых веществ на поверхности воды). Этим объясняется радужная окраска перьев павлина, крыльев бабочек, переливы цветов на некоторых этикетках.

 

В лаборатории имеются две экспериментальные установки: одна с газовым (гелий-неоновым) лазером, другая с полупроводниковым лазером. Схема установки с газовым лазером показана на рис. 3, с полупроводниковым лазером – на рис. 4. На обеих схемах изображены: лазер 1, линза 2, экран 3 и плоскопараллельная пластина 4. На установке с полупроводниковым лазером, кроме того, предусмотрен защитный экран 5.

Несмотря на то, что установки отличаются конструктивно, методика эксперимента для них одинакова.

 

Приборы и принадлежности: лазер; оптическая скамья с установленными на ней линзой, экраном, стеклянной пластиной.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

 

ВНИМАНИЕ! Попадание в глаза прямого лазерного излучения опасно для зрения. При работе с лазером его свет можно наблюдать только после отражения от рассеивающих поверхностей.

Вариант установки (с газовым или полупроводниковым лазером) задается преподавателем или индивидуальным заданием.

Лазер включает и выключает только преподаватель или лаборант.

 

1. Установите стеклянную пластину 4 на заданном (преподавателем или индивидуальным заданием) расстоянии от экрана 3. Линейкой измерьте толщину  стеклянной пластины 4. Значения   и   запишите в тетрадь.
2. С помощью преподавателя или лаборанта добейтесь появления на экране системы темных и светлых интерференционных колец.
3. Закрепите на экране 3 лист бумаги с вырезанным в нем отверстием для прохождения света. Отметьте на листе положения первых 5-10 тёмных колец. Для этого карандашом нанесите метки по вертикальному и горизонтальному направлениям по одну и другую сторону от центра картины.
4. Снимите бумагу и линейкой по нарисованным меткам измерьте диаметры темных колец по вертикальному ( ) и горизонтальному ( ) направлениям. Результаты измерений под соответствующими номерами колец занесите в табл. 1.
5. Для каждого порядка интерференции сначала вычислите средний диаметр кольца , затем радиус кольца и его квадрат . Результаты вычислений занесите в табл. 1.

 

 

Таблица 1

Номер кольца	Диаметр кольца , мм			, мм	, мм2
	(по вертикали)	(по горизонтали)	(средний)
1	10	9
2	17	15
3	21	20
4	24	23
5	27	27
6	30	30
7	32	33

 

l = 450 мм   ,     d  = 19,5 мм   ,    λ  = 0,670 мкм

6. Постройте график зависимости величины от номера  кольца, откладывая   по вертикальной оси,  – по горизонтальной оси. По характеру расположения экспериментальных точек определите, группируются ли они около прямой линии, как предсказывает теоретическая формула (9). Если да, то проведите по линейке прямую линию, стараясь, чтобы она проходила как можно ближе к каждой из экспериментальных точек. (Проведенная прямая линия может не проходить через все экспериментальные точки).

m

rm2,мм2

Образец графика

7. Для нахождения углового коэффициента полученной прямой определите значения и  для двух точек, лежащих на проведенной прямой, которые соответствуют первому и последнему кольцам с номерами  и . Рассчитайте угловой коэффициент по формуле

.

8. По формуле (11) рассчитайте показатель преломления стекла.

 

Длина волны излучения газового лазера  0,6328 мкм, полупроводникового лазера 0,670 мкм.

9. Рассчитайте погрешность определения показателя преломления по формуле , где

;   ;

;   .

= _____

=_____

Погрешность длины волны  находится как погрешность величины, заданной численно. Погрешности измерений толщины  пластины и расстояния  от пластины до экрана равны приборным погрешностям линейки.

Погрешность  определите следующим образом. Сначала на графике найдите экспериментальную точку, которая максимально отклоняется от проведенной прямой. Затем определите величину , которая равна отклонению этой точки от прямой по вертикальной оси в единицах этой оси (т.е. в мм²).

10. Найденное значение показателя преломления стеклянной пластины запишите в виде доверительного интервала

n = ____ + _____

11. В заключении по работе:

• Приведите полученный доверительный интервал .
• Укажите, измерение какой из величин вносит основной вклад в погрешность величины .
• Сравните полученный результат с табличным значением показателя преломления стекла (табл. 2).

Вывод: измерили показатель преломления стекла с помощью интерференции света на плоскопараллельной пластине n = ____ + ____; табличное значение показателя преломления стекла __________ в полученный доверительный интервал; основной вклад в погрешность измерения показателя преломления внесла ошибка измерения _______________________.

 

Таблица 2

Показатель преломления   оптического стекла (крон) для нескольких длин волн

 

, мкм	0,65                             0,6                              0,5
	1,515                          1,518                         1,524

 

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

 

1. В чем заключается явление интерференции света?
2. При каком условии интерференционная картина будет устойчивой, т.е. неизменной с течением времени?
3. Каково условие когерентности двух световых волн, полученных от одного и того же лазера?
4. Что такое разность хода? Как она создается в условиях данной работы?
5. Каковы условия минимумов и максимумов интенсивности света в интерференционной картине?
6. Что такое показатель преломления? Показатель преломления какой среды равен единице?
7. Какова роль линзы 2 в оптической схеме на рис. 2 и рис. 3?
8. Выведите соотношения (8) и (9).
9. Почему расчеты по формуле (11) дают правильные результаты, хотя измеряемый номер кольца не совпадает с порядком интерференции ?
10. В данной работе максимальный порядок интерференции равен максимально возможному числу наблюдаемых темных колец. Вычислите величину , приняв α = 0; n = 1,5; d = 20 мм; λ = 0,67 мкм.

 

 

Вывод формулы для разности хода  лучей при интерференции

света на плоскопараллельной пластине

 

Пусть  и  – оптические длины световых лучей ОВА и ОDA (рис. 5). Используя этот рисунок, находим

,                 (12)

,             (13)

где  – длина волны лазерного излучения,  – показатель преломления стекла пластины. Потеря половины длины волны в выражении (12) связана с отражением света от оптически более плотной среды. По определению разность хода , т.е.

.                            (14)

Если  – угол преломления луча ED в пластине, то

,

где  – толщина пластины. Углы падения  и  лучей OB и OE близки друг к другу, отсюда

.

На основании закона преломления света

.                                         (15)

Используя тригонометрические соотношения

из выражений (14) и (15) окончательно получаем

.                                      (16)

 

[1] Устройство и принцип действия электронного осциллографа см. в ПРИЛОЖЕНИИ (с. 263).

[2] Вывод формулы (5) см. в конце данной работы: с. 149.